Định lý Đào (conic)
Định lý Đào (conic) là một định lý trong lĩnh vực hình học phẳng, nói về sự tồn tại của một đường thẳng trong cấu trúc hình học liên quan đến đường conic và cực và đường thẳng đối cực. Định lý Đào có thể suy biến thành một trong nhiều định lý nổi tiếng trước đó gồm: đường thẳng Droz-Farny, định lý Goormaghtigh, định lý Đào (hẹp), định lý Zaslavsky, định lý Colling, định lý Carnot, vấn đề Bliss, định lý Nixon [1][2][3][4][5]
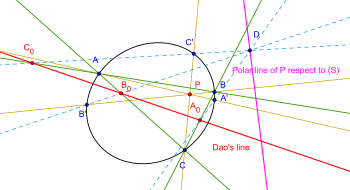
Nội dung định lý
sửaCho đường conic (S) và điểm trên mặt phẳng, ba đường thẳng qua cắt đường conic lần lượt tại các điểm ; ; . Cho là một điểm nằm trên đường thẳng đối cực của hoặc trên đường conic (S) thì lần lượt cắt ba cạnh tại ba điểm thẳng hàng. Hơn thế bốn điểm thẳng hàng khi và chỉ khi nằm trên đường conic (S).[1][6][7]
Trong trường hợp điểm nằm trên đường conic . Gọi cắt tại . Gọi đường thẳng đi qua và song song với cắt tại . Gọi là điểm trên đường thẳng sao cho . Định nghĩa các điểm một cách tương tự. Khi đó bảy điểm , thẳng hàng.[8]
Lịch sử
sửaĐịnh lý này được phát hiện và chứng minh bởi nhiều người, cụ thể như sau:
- Trường hợp điểm D nằm trên đường thẳng cực của điểm P do Đào Thanh Oai phát hiện được đăng tại Advanced Plane Geometry Message 1307 năm 2014[9] và được chứng minh trong bài báo của Nguyễn Ngọc Giang.[1] Một trường hợp đặc biệt của trường hợp này là điểm P nằm trên đường thẳng đối cực và nằm tại vô cùng được Đào Thanh Oai đề xuất tại Advanced Plane Geometry Message 1271 năm 2014.[10] Điều này được chứng minh trong một bài báo của Trần Hoàng Sơn.[11]. Một bài báo của tác giả Nguyễn Minh Hà xác nhận rằng trường hợp riêng này cũng được Trần Quang Hùng tìm ra độc lập.[12]
- Trường hợp điểm D nằm trên đường conic được Đào Thanh Oai phát biểu chứng minh vào tháng 6 năm 2013 trên Cut-The-Knot[7] và diễn đàn toán học phổ thông "Art of Problem Solving"[2]. Bài báo của Nguyễn Ngọc Giang cũng đề cập đến trường hợp này nhưng không chứng minh. Trong trường hợp này định lý cũng được giáo sư Geoff Smith đăng trên tạp chí the Mathematical Gazette và ông đã xác nhận sự phát hiện lặp lại của mình với Đào Thanh Oai.[6] Trường hợp đường conic là đường tròn phần đảo được nêu trước đó rất lâu bởi Paul Aubert và Joseph Neuberg.[13]
Xem thêm
sửaTham khảo
sửa- ^ a b c Nguyen Ngoc Giang, A proof of Dao theorem, Global Journal of Advanced Research on Classical and Modern Geometries, ISSN: 2284-5569, Vol.4, (2015), Issue 2, page 102-105
- ^ a b Dao Thanh Oai, Luis Gonzalez, A Generalization Simson's line, Collings theorem tại Art of Problem Solving
- ^ O.T.Dao, Advanced Plane Geometry Message 2807, ngày 17 tháng 9 năm 2015.
- ^ Tran Minh Ngoc, A Purely Synthetic Proof of Dao’s Theorem On A Conic And Its Applications Lưu trữ 2020-11-16 tại Wayback Machine International Journal of Computer Discovered Mathematics, November 2018, Volume 3, pp.145-152,
- ^ Nguyen Minh Ha, SYNTHETIC PROOF OF DAO’S THEOREM, Global Journal of Advanced Research on Classical and Modern Geometries, ISSN: 2284-5569, Vol.9, (2020), Issue 1, page 20-23
- ^ a b Geoff Smith (2015). 99.20 A projective Simson line. The Mathematical Gazette, 99, pp 339-341. doi:10.1017/mag.2015.47
- ^ a b O.T.Dao 29-July-2013, Two Pascals merge into one, Cut-The-Knot
- ^ Dao Thanh Oai, Generalizations of some famous classical Euclidean geometry theorems International Journal of Computer Discovered Mathematics, Volume 1 (September 2016) Number 3, pp.12-20.
- ^ O.T.Dao, Advanced Plane Geometry Message 1307, ngày 22 tháng 5 năm 2014
- ^ O.T.Dao, Advanced Plane Geometry Message 1271, ngày 26 tháng 4 năm 2014.
- ^ Tran Hoang Son, A synthetic proof of Dao's generalization of Goormaghtigh's theorem, Global Journal of Advanced Research on Classical and Modern Geometries, ISSN 2284-5569, volume 3, pages 125–129
- ^ Nguyen Minh Ha and Pham Nam Khanh, Another simple proof of the Goormaghtigh theorem and the generalized Goormaghtigh theorem, Journal of Classical Geometry, Volum 4.
- ^ Jean Louis AYME, LA P-TRANSVERSALE DE Q
Đọc thêm
sửa- Nhiều tác giả, chuyên đề Đường vào hình học sơ cấp số 2, năm 2021, nhà xuất bản Thanh Niên.
- Nguyễn Ngọc Giang, Lê Viết Ân, Sáng tạo mới trong hình học, năm 2022, Nhà xuất Bản đại học Quốc gia Hà Nội.
- Bamberg, John (2023). Analytic Projective Geometry. Nhà xuất bản Đại học Cambridge. tr. Theorem 10.27. ISBN 978-1-009-26059-6.