Nhóm con Frattini

Trong toán học, cụ thể hơn là trong lý thuyết nhóm, nhóm con Frattini $\Phi (G)$ của nhóm $G$ là giao của tất cả nhóm con tối đại của $G$ . Nếu $G$ không có nhóm con tối đại nào, ví dụ như $G$ là nhóm tầm thường {e} hoặc nhóm Prüfer, thì $\Phi (G)=G$ . Nó tương tự với căn Jacobson trong lý thuyết vành, và theo trực giác thì có thể coi nhóm là nhóm con chứa "phần tử nhỏ" (xem dưới). Nhóm được đặt tên theo Giovanni Frattini, người định nghĩa khái niệm này trong bài viết năm 1885.^[1]

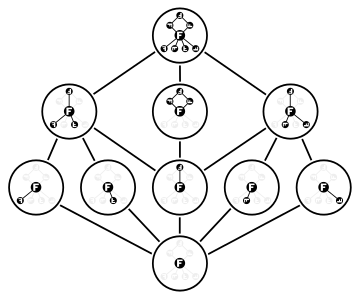
Một số tính chất sửa

$\Phi (G)$ bằng với tập các phần tử không sinh của $G$ . Phần tử không sinh của $G$ là phần tử luôn có thể bỏ đi được trong tập sinh; thức là nếu a là phần tử của $G$ sao cho nếu $X$ là tập sinh của $G$ chứa a, thì $X\setminus \{a\}$ cũng là tập sinh của $G$ .
$\Phi (G)$ luôn là nhóm con đặc trưng của $G$ ; cụ thể hơn, nó luôn là nhóm con chuẩn tắc của $G$ .
Nếu $G$ hữu hạn, thì $\Phi (G)$ là nhóm lũy linh
Nếu $G$ là p-nhóm hữu hạn, thì $\Phi (G)=G^{p}[G,G]$ . Do đó nhóm con Frattini là nhóm con chuẩn tắc nhỏ nhất N sao cho nhóm thương $G/N$ là nhóm abel sơ cấp, đẳng cấu với tổng trực tiếp của các nhóm cyclic có cấp p. Hơn nữa, nếu nhóm thương $G/\Phi (G)$ (hay còn gọi là thương Frattini của $G$ ) có cấp $p^{k}$ , thì k là số phần tử sinh nhỏ nhất của cấp $G$ (tức là lực lượng nhỏ nhất của tập sinh cho $G$ ). Mặt khác, một p-nhóm hữu hạn là nhóm cyclic khi và chỉ khi thương Frattini của nó cũng là nhóm cyclic (với cấp p). p-nhóm hữu hạn là nhóm abel sơ cấp khi và chỉ khi nhóm con Frattini của nó là nhóm tầm thường, $\Phi (G)=\{e\}$ .
Nếu $H$ và $K$ hữu hạn, thì $\Phi (H\times K)=\Phi (H)\times \Phi (K)$ .

Ví dụ nhóm có nhóm con Frattini không tầm thường là nhóm cyclic $G$ có cấp $p^{2}$ , trong đó p là số nguyên tố, sinh bởi a, $\Phi (G)=\left\langle a^{p}\right\rangle$ .

Xem thêm sửa

Tham khảo sửa

^ Frattini, Giovanni (1885). “Intorno alla generazione dei gruppi di operazioni” (PDF). Accademia dei Lincei, Rendiconti. (4). I: 281–285, 455–457. JFM 17.0097.01.

Hall, Marshall (1959). The Theory of Groups. New York: Macmillan. (See Chapter 10, especially Section 10.4.)

[1] Frattini, Giovanni (1885). “Intorno alla generazione dei gruppi di operazioni” (PDF). Accademia dei Lincei, Rendiconti. (4). I: 281–285, 455–457. JFM 17.0097.01.

[1]